Computational Thinking in Mathematics

Together mainly with Eric Muller (Professor Emeritus, Brock University), we have been examining diverse aspects of a sustained implementation since 2001 at our department of mathematics and statistics: In a sequence of three undergraduate mathematics courses, students learn to design, program, and use interactive computer environments for the systematic investigation of mathematical concepts, conjectures, theorems, or real-world situations. These courses have been called MICA I-II-III (Mathematics Integrated with Computers and Applications).


We have focused on:

  • Student Learning Experience

    • Students constructionist experiences of learning mathematics (Buteau et al. 2016; 2014)
    • Students developing proficiency in what is called the third pillar of scientific inquiry of complex systems (European Mathematical Society, 2011): Together with theory and experimentation, a third pillar of scientific inquiry of complex systems has emerged in the form of a combination of modeling, simulation, optimization and visualization”. (Buteau et al. 2016)
    • Students developed competencies (2014a,b; 2013)
    • Students original programming-based mathematics projects (Muller et al., 2009)

  • Pedagogy and Course Design Analysis

    • Instrumental integration of programming in the introductory MICA I course (Buteau & Muller, 2014)
    • Pedagogical strategies (Muller et al., 2009; Buteau, Muller, & Ralph, 2015)

  • Task Analysis

    • Task analysis of creating and using interactive computer environments for the systematic investigation of mathematical concepts, conjectures, theorems, or real-world situations (Buteau & Muller, 2010)

  • Assessment

    • Assessment of mathematics in programming-based mathematical tasks and assessment of computational thinking development throughout the MICA course sequence (Buteau & Muller, submitted)

  • Teacher Education

    • Future mathematics teachers engagement, ownership, and pride in creating and testing original interactive environments for the learning of school mathematics concepts (Mgombelo & Buteau, 2009; 2010)
    • Future mathematics teachers original interactive environments for the learning of school mathematics concepts (Muller & Buteau, 2005)

  • MICA courses: a concrete implementation of microworlds? Computational thinking? Constructionism?

    • How the students, teaching assistants, individual faculty, and the department perceive the nature of MICA courses (Buteau et al. 2014; 2015)
    • It is mathematics practice that, we argue, falls under the third pillar of scientific inquiry of complex systems, namely: Together with theory and experimentation, a third pillar of scientific inquiry of complex systems has emerged in the form of a combination of modeling, simulation, optimization and visualization (European Mathematical Society, 2011); Buteau et al. (2016a,b)
    • An implementation of implicit constructionist nature (Buteau et al., 2015, 2016; Muller et al., 2015)
    • It is about learning experimental mathematics, learning mathematics by programming and simulation, and through inquiry-based learning approach (Marshall 2013; Marshall & Buteau, 2014)
    • Student projects are of microworld type (Marshall & Buteau, 2014; Marshall et al., 2013, 2014)
    • It falls under the larger context of computational thinking (Buteau & Muller, submitted)
Ramona, undergraduate student
"Both creating and working with this program has assisted me to fully grasp the way a dynamical system works by observing the table, the graphs, and the cobweb with countless test values for a, b, and x0."

- Ramona, Undergraduate Student
(as reported in Buteau, Muller, Marshall, Sacristán, & Mgombelo, 2016)

"do things with a computer that would be impossible without it"
(Healy & Kynigos, 2010)

This was about Ramona’s cohort third project assignment for which they had to create an environment (in vb.net) to explore the dynamical system based on a cubic (two parameters involved), and describe its behaviour. In lectures, they were introduced to discrete dynamical systems. In labs, students were guided to create an interactive environment about the logistic function (one parameter involved), and, through an interactive lab session, to systematically explore its behaviour.

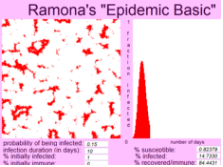
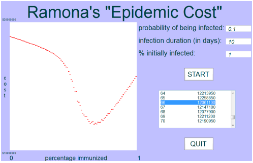Second-year student Ramonas 2013 cohort was asked to create (in vb.net) simulations of epidemics to examine the effects of inoculation on the spread of epidemics, and their cost. Students, like Ramona, experienced real-time simulations of required case scenarios, and reported their results in written reports. Building on a simulation of a specific epidemic to estimate ist related costs, for example Ramona found that her estimate the percentage of immunized people that minimizes the cost the epidemic is 67% by inspection in which the cost is $12,078,150. (as reported in Buteau, Muller, Marshall, Sacristán, & Mgombelo, 2016

"people construct new knowledge with particular effectiveness when they are engaged in constructing personally meaningful products...[i.e.,] something meaningful to themselves and to others around them"
(Kafai & Resnick, 1996, p. 214)

Students in each MICA course end by an original project, done individually or in pairs, and in which they choose their own project. Here are some examples:

Structure of the Hailstone Sequence



Simulation of the effects on the economy of central banks' monetary policy



Encryption Pseudorandom-ness Explorer



Simulation of rowing-boat running time



Is it better to walk or run in the rain?



Technology in University Math Education

We have investigated the integration of Computer Algebra Systems (CAS)-based technology in post-secondary mathematics instruction. Funded by SSHRC International Opportunities Fund Grants, 2007 - 2010) and together with Dr. Daniel Jarvis (Faculty of Education, Nipissing University) and Zsolt Lavicza (Faculty of Education, University of Cambridge, UK), we have conducted an international research project that includes three main parts:

  • a national survey on Canadian mathematicians practices (Buteau et al., 2013);
  • a comprehensive literature review (Marshall et al., 2010; Buteau et al, 2010); and
  • two case studies of mathematics departments that have integrated and sustained over time the use of technology in its teaching (Jarvis et al., 2015)

    • Jarvis, Buteau & Lavicza, North Bay, 2007

    Selected results:

    Our Canadian survey (n=302) that took place in 2009 about mathematicians’ practices with computer algebra systems (CAS) indicated that a great proportion Canadian mathematician participants (81%) use CAS at least once a month in their research whereby a smaller yet significant proportion (69%) uses CAS in their teaching.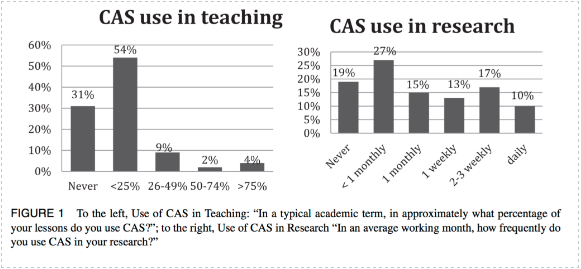
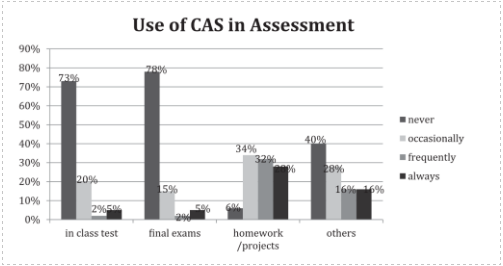    "     FIGURE (Buteau, Jarvis, & Lavicza, 2014, p. 41). On the top, use of CAS in teaching: "In a typical academic term, in approximately what percentage of your lessons do you use CAS?; to the bottom, use of CAS in research In an average working month, how frequently do you use CAS in your research?"

    “Most of us came to the view that mathematics is an “alive subject,” it’s not dead, you know, and that new technologies have opened up new branches of mathematics. When our students go out to get jobs they will be using technology, and so we have to incorporate that at a very fundamental level into what we teach.”
    (participant’s response from our case study of two mathematics departments)


    Our case study about two mathematics departments in which the sustained use of technology was strategically established in a mathematics degree program indicate that “sustained implementation at the departmental level requires a unique combination of key factors such as: a dedicated core group led by a committed advocate in a position of influence/power; a strong and shared incentive for change; strategic hiring processes; an administration which supports creative pedagogical reform and well-considered risk-taking; and, a continuous and determined revisiting of the original vision and purpose.” (Jarvis, Lavicza, & Buteau, 2013, p. 117)

    “I worked as a mathematician for [many] years in research and industry. I KNOW what a mathematician needs to know to be useful to society (i.e., have a job). Either you know how to use a computer, or you flip burgers.”

    - Participant Response from Nation-wide Survey


    Math Computer Game: E-Brock Bugs

    In a joint work with Eric Muller and Laura Broley, I have recently been interested in the area of good instructional mathematics game design. This has led us to design E-Brock Bugs©, a free online computer game about basic probability, and to conduct research involving the game. Our interest is focused on epistemic games, i.e., games “where players think and act like real world professionals” (Bagley & Shaffer, 2009, p.36). Thus in epistemic mathematics games, "[t]he player becomes a mathematician and problem solver within the context of the game" (Offenholly, 2011, p. 45).



    "a player [in a well-designed instructional game] is not being asked to 'learn how to do X'. Rather, it is all about 'becoming a (better) X-er'"
    (Devlin, 2011, p. 126).

    We are interested in researching the impact on students of playing epistemic mathematics games. Insofar, we have limited our work to E-Brock Bugs computer game and have focused on: i) the theoretical analysis of the game design; ii) impact on mathematics achievement and motivation (exploratory study); and iii) players’ mathematical identity and engagement. Our most recent ongoing work has involved 61 students from three Grade 12 data management (MDM4U) classes in which playing E-Brock Bugs was part of the course workload and assessment.



    E-Brock Bugs©, created by Laura Broley (middle) with Chantal Buteau (right) and Eric Muller (left), is a computer game with roots originating in Brock Bugs, a probabilistic board game created in early 1980s by Eric Muller.

    Related Publications:

    Muller,E, Broley, L., & Buteau, C. (in press). Struggles and Growth in Mathematics Education: Reflections by three Generations of Mathematicians, Creators of the Computer Game E-Brock Bugs. Journal of Humanistic Mathematics.

    Broley, L., Buteau, C., & Muller. E. (2015). E-Brock Bugs©: An Epistemic Computer Game.Journal of Humanistic Mathematics, 5(2), 3-25.

    Mancuso, A. (2014). The effect the computer game, E-Brock Bugs, has on student achievement and motivation in Mathematics students and different genders. Unpublished Honour’ s Thesis, Brock University, St.Catharines (Canada).

    Buteau, C., Broley, L., & Muller, E. (2014). E-Brock Bugs: An Epistemic Math Computer Game. In Proceedings of Joint Meeting Int. Group Psychology of Mathematics Education (PME 38), July 2014, Vancouver, Canada.

    Broley, L., Buteau, C., & Muller, E. (2013). E-Brock Bugs: A New Free Online Math Computer Game for the Development of Mathematics Thinking - Integrating Probability Concepts in MDM4U (slides). Invited presentation at Fields MathEd Forum, Toronto (Canada), November 2013.

    Broley, L. (2013). E-Brock Bugs: The Creation and Analysis of an Epistemic Mathematics Computer Game. Unpublished Honour’ s Thesis, Brock University, St.Catharines (Canada).

    Math and Music

    "Music cannot be degenerated or reduced to a section of Mathematics: Music is fundamentally rooted within physical, psychological and semiotic realities. But we need more sophisticated methods besides statistical and empirical data in order to formally describe musical instances."
    (Pierre Boulez)

    I have been conducting research on deterministic modeling of music analysis and structure and computational music analysis. I am particularly interested in modeling motivic (melodic) structure and analysis of musical compositions through a topological approach.

    The motivic analysis of a music composition consists of identifying the short melody, called a motif, that units the composition through its strict repetitions, the so-called imitations, and its variations and transformations which are heard throughout the whole composition. Mainly using group theory, linear algebra and general topology concepts, we construct a (T_0-) topological structure corresponding to the motivic hierarchy of a composition. Our (computationnal topology) implementation (JAVA), called Melos, can analyze music compositions such as Schumann’ s Träumerei from Kinderszenen.

    My ongoing interdisciplinary research mainly concerns:
    • Concrete applications to a music corpus (recent works include Brahms' Op.51 No.1 and Schumann's Kinderszenen)
    • A categorical extension of our model including e.g. continuous functions between two motivic spaces, products of different spaces, natural transformations (gestalt spaces);
    • Visualisation of Melos’multiple outputs in order to show and hear, and to explore mathematics and music results: now in our OM-Melos tool (see Buteau & Vipperman, 2008);

    One of our visualization of the topological structure is done through what weve called Weight graphs whereby the height represents a measure of the motivic significance of a motif (of gestalt, i.e., class of a motif). In this representation, the higher the more significant.



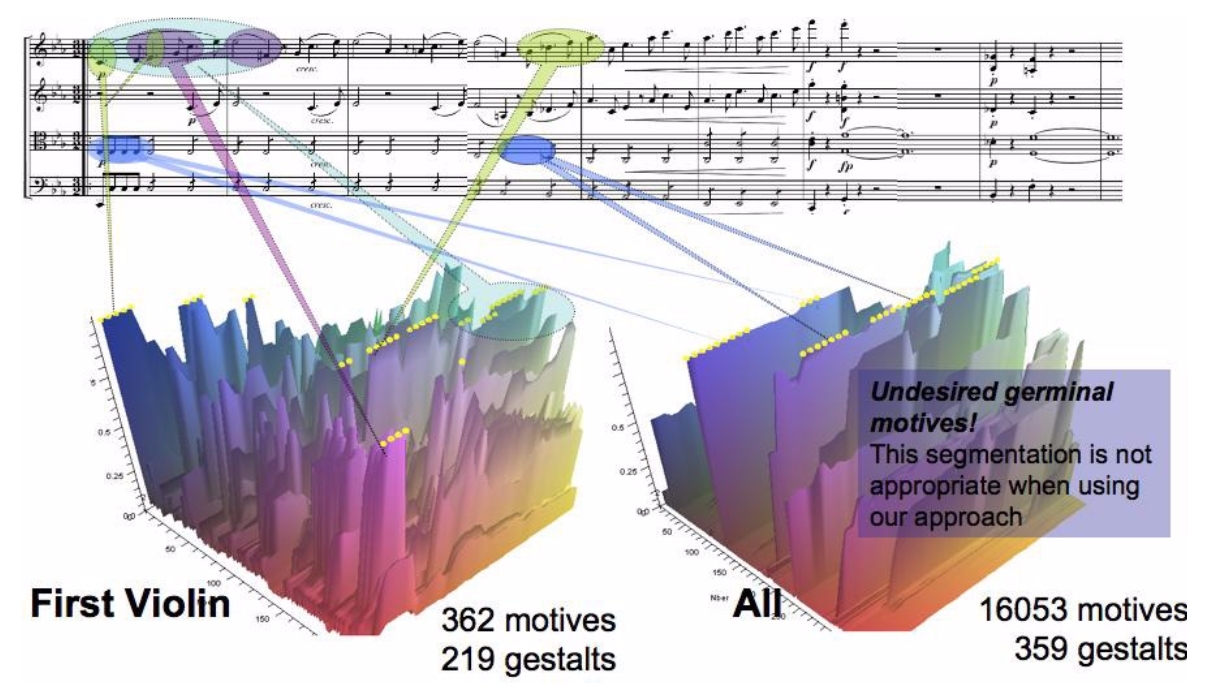
    Figure (taken from Buteau & Anagnostopoulou, 2011) that highlights the issue of segmentation in computational music analysis. The figure shows the weight function graphs for two analyses of the same piece, the 10 opening bars of Brahm’s String Quartet Op.51 No.1 first movement, with same analytical parameters (t = Dia, P = Id, d=absolute value distance functions, weight=Mazzola weight), but with different segmentations. To the right, the segmentation considers all four voices, whereas to the left motives strictly stem from the first violin voice. Weight graphs, automatically produced by the Maple implement, give an overall picture of the dynamic motivic landscape: the peaks (yellow dots) correspond to gestalts (front axis) with highest weights (vertical axis), i.e., germinal motives, as the similarity threshold grows (horizontal axis). The analyzed score section has been manually added for clarity purposes. The actual motives with peaks in the weight graph are represented as notes in the score through the implement in OpenMusic.



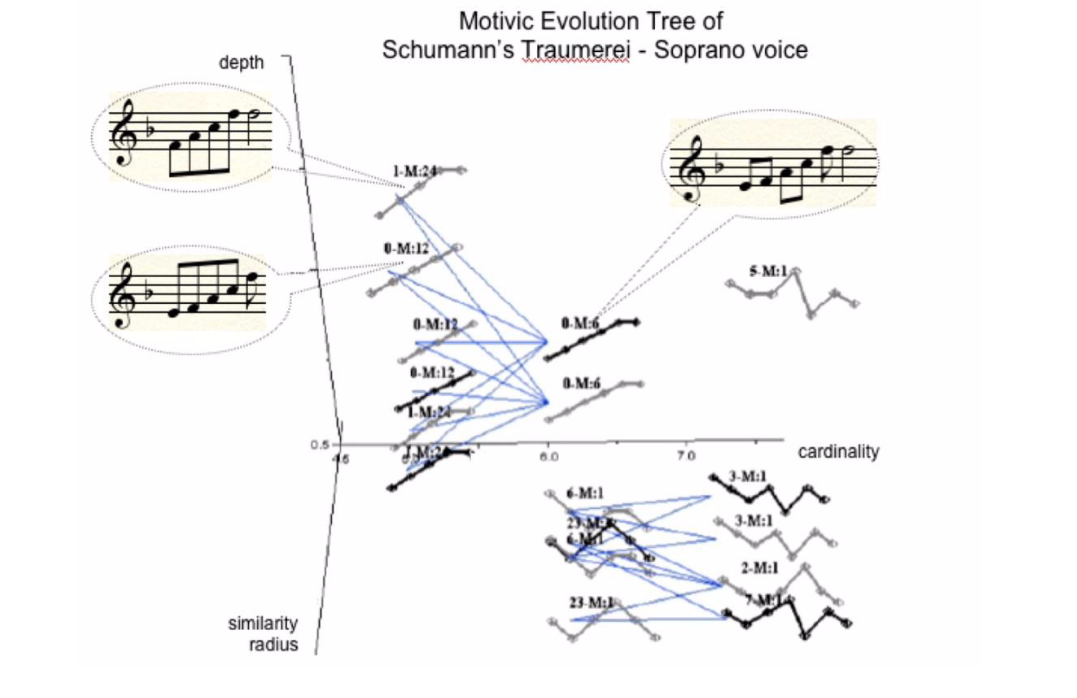
    Figure (taken from Buteau & Vipperman, 2008) showing what we’ve called the motivic evolution tree three-dimensional representation of Schumann’s Traümerei in which three significant motives were manually stressed, according to the topological approach given an analytical setting (t = Com, P = transpositions and translations in time only, and d =relative Euclidean distance). In black, the most significant motives; in grey, the second most significant ones. Submotive relations are represented by lines linking the respective motives.